mikeg's blog

Blocked waiting for my either the software development group to give me new code to test or my FreeBSD build VM to give me a new OS build to test, so how about some random thoughts on programming?

I've reached the inescapable conclusion that all software development cycles can be expressed as a single equation: y=tan(x+(π/2))

X represents time (on a totally non-linear scale) with each interval of width π being the development of a software release and the zero point where the function crosses the X axis representing the release of the X/π^th version.  The Y axis represents the state of the code - how "bug free" it is.  I'll call the Y value within a version the "completeness" of the code for simplicity.

This functional model actually works surprisingly well:

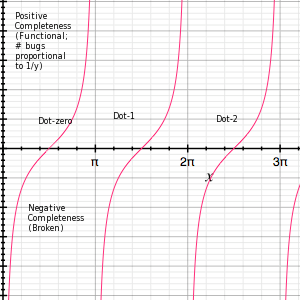
• During pre-0.0 release (X|0...π/2) the software is riddled with bugs and brokenness ("completeness" is negative - that shit don't work!).
  • At some point (X=(π+ε)/2) the software becomes at least functional (miniscule positive completeness), and is released to the unsuspecting public.
  • The initial release is buggy as shit, and massive patching and bug fixing happens
    (This is roughly from X|(π+ε)/2...3π/2 -- For the sake of argument let's call the 3π/2 mark the .1 release, or in MS parlance, "Service Pack 1")
  • The software continues asymptotically approaching infinite completeness -- that nirvana state of having no bugs...
• ...At which point Marketing comes along and says the users want new features -- On our graph this corresponds to one of the vertical asymptote at multiples of π.
  • Development begins on the next (N/π)-dot-zero release, starting al over again from negative completeness.

In practical terms software development is not a true function: Each development window is independent and shifted toward X=0, with some overlap between the currently released version and the version under development.